如何理解薛定谔方程?
本文较为硬核,请酌情跳过部分内容。
不过,若是你真想理解薛定谔方程,我建议你全看完。
薛定谔:德布罗意的论文是在说,波可以是粒子,粒子也可以是波。
德拜:有了波,就要有个波动方程。
薛定谔:我试试。

德布罗意方程组二十世纪初,物理学界有一项大发现:
光,具有波粒二象性。
(可以用波动模型去描述光,也可以用粒子模型去描述光。)
这启发了德布罗意,于是这位公子提出了物质波的思想。
简单地说,人们习惯于将原子、电子这些实物用粒子模型去描述,而忽略了它们的波动属性。

(这可不是一拍脑门儿就想出来的,而是德布罗意对哈密顿力学的深刻理解的体现。)
为此,德布罗意还写出了这些实物对应的波的频率和波长的公式:

这两个公式被称为德布罗意方程组。
f是波的频率。
E是微观粒子的能量。
λ是波的波长。
p是微观粒子的动量。
h是普朗克常数。
h=6.62606896×10^(-34) J·s
这种波后来被称为物质波,而薛定谔方程就是在描述物质波,主要用于描述电子的物质波。
(电子、原子、石头、炮弹、星球、……,都可以被看成是物质波。)
经典的波函数物理学的精髓是描述,最好是用数学语言描述。
如何用数学语言描述物质波呢?
别急,咱们先看看如何用数学语言描述经典的波。
你可能会问:上面的德布罗意方程组,难道没有用数学语言描述物质波吗?
可以说,描述地不完整。
至于怎么不完整?
还是要从经典的波谈起。
波是振动形式在空间中的传递,想要描述波,就要先描述振动。
如何描述振动?
首先要清楚,振动有三个要素:
幅值、频率、相位。
着重介绍一下相位,相位就是振动周期中的一个时刻。比较多个振动的先后顺序的时候,就是在比较相位。
这三个要素可以被振动函数整合到一起。
在这里只考虑最简单的振动:简谐振动。
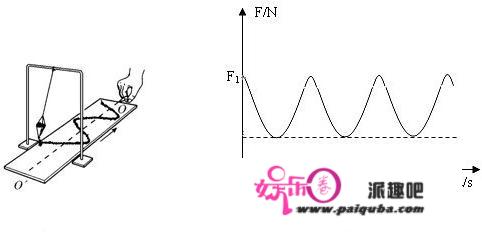
简谐振动的振动函数是正弦函数(也可以是余弦函数)。
先看一下最简单的正弦函数:

为它添加三个参数,就形成了振动函数:
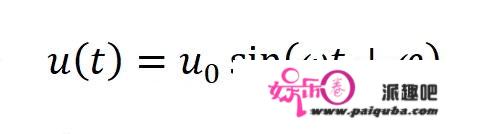
u_0表示幅值。
ω表示角频率,和频率有相同的单位。
(ωt+φ)表示相位,其中的φ表示初始相位。
振动的三个要素,都被包含在振动函数里。
振动函数只有一个自变量,就是时间:t
(为了待会儿和波函数比较,我需要在这里使用偏向于数学的语言。)
那么,如何描述一个波?
波有五个要素:
幅值、频率、波长、波速、相位。
和振动相比,多了波长和波速。
这五个要素可以被经典的波函数整合到一起。
频率、波长、波速这三个量,只有两个是独立的,知道任意两个,就可以求出第三个。
所以,暂时可以减去一个要素,只关注其中的四个要素。
经典的波函数自然也要包含这四个要素:
幅值、相位,以及频率、波长、波速中的任意两个量。
为了进一步简化问题,这里介绍一维的波函数,波只朝一个方向传播。
并且,不考虑波的衰减,波的幅值不变。
在这里只考虑最简单的波:简谐波。
(任意波形的波,都能由一系列的简谐波叠加而成。)
简谐波是简谐振动在空间中的传递,可以从简谐振动的振动函数出发,推导出简谐波的波函数。
由于简谐波在空间中传播,因此它有有两个自变量,时间:t、距离:x。
对于一个以波速v传播的简谐波,例如下图:
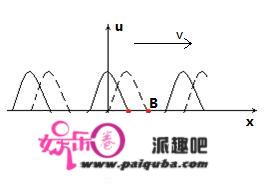
A点离波源较近,B点离波源较远,因此B点比A点的相位要滞后。
如果分别写出A点和B点的振动函数,那么将A点的振动函数向右平移就可以得到B点的振动函数。
(左加右减,基本的数学知识还是要有的。)
向右平移的“距离”,就是简谐波从A传到B所需的时间。
(距离除以波速就是这个时间。)
以此类推,可以写出波速为v,与波源距离为x的点的振动函数。
这其实就是波函数:
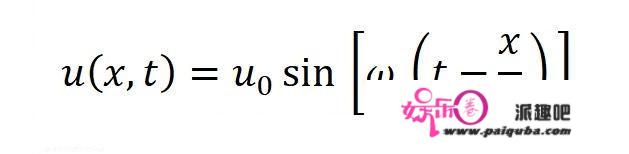
为了和上面的德布罗意方程组衔接,把波函数写成用频率f和波长λ表示的形式。
利用这两个公式,可以把角频率ω和波速v替换掉。
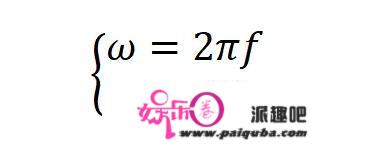
(有高中物理的基础的话,对这两个公式应该很熟悉。)
可以得到:
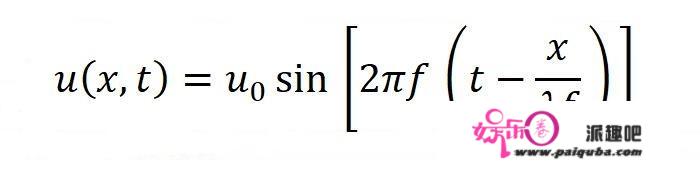
整理一下:
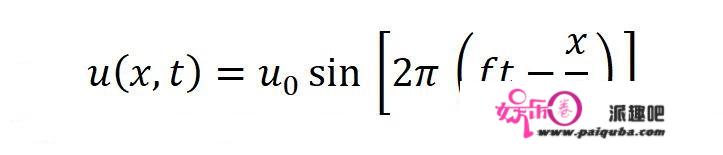
观察一下经典的波函数,它整合了我们关注的四个要素,所以它完整地描述了经典的波。
还可以利用欧拉公式:
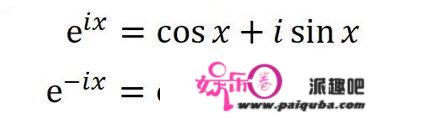
(i是虚数单位,i的平方等于-1。)
把经典的波函数写成复指数形式:
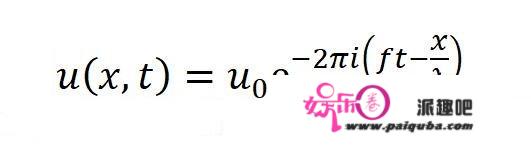
(指数项前面有个负号,这只是个习惯,也可以不带负号。)
有不少读者反应:不理解把波函数写成复指数形式的过程。
笔者在此详细说明一下:
(部分读者可以酌情跳过。)
首先需要一个公式:

(后面会说到这个公式的意义。)
把上面的那两个欧拉公式分别相加和相减,会得到:
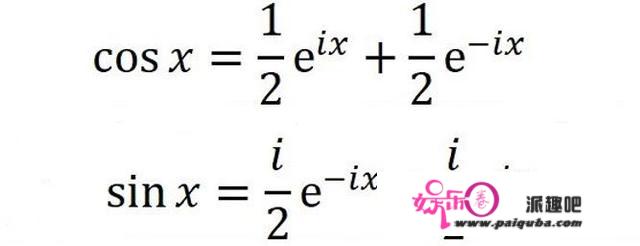
在这里简单介绍一下复数和复平面:
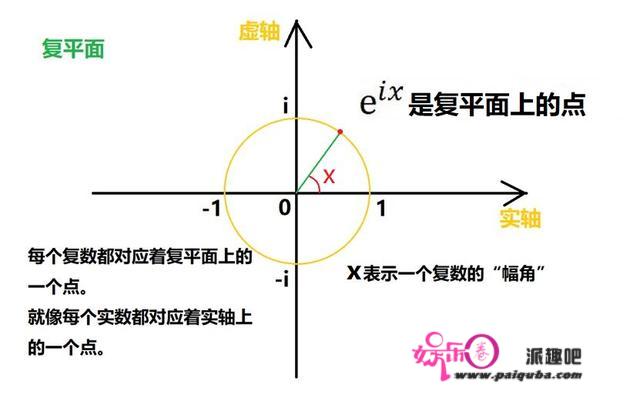
依葫芦画瓢,可以得到下面这个公式:

所以可以得到:
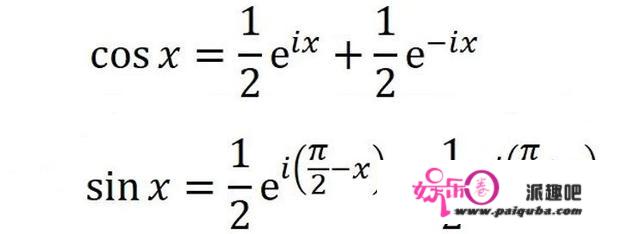
然后我们需要知道的是:

任意波形的波,都能由一系列的正弦波相加而成!
把正弦函数或余弦函数写成复指数形式以后,我们可以发现:
一系列的正弦波相加,其实就是一系列的复指数函数相加。
所以,可以把任意一个波的“最小单元”看成是:复指数函数。
(我们之前用正弦函数代表波,也是因为可以把任意一个波的“最小单元”看成是正弦函数。)
这样一来,我们也可以用复指数函数来表示波:
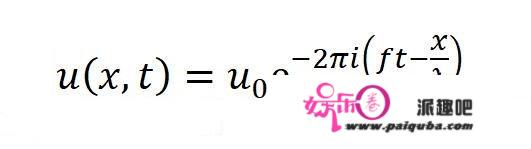
波函数的复指数形式的内容是为了最终推导薛定谔方程做铺垫。
至于为什么要写成复指数形式,是因为对相位的表达更加方便。
波函数是正弦函数(余弦函数),而正弦函数(余弦函数)的导数仅仅只是相位超前了90度。
(导数就是变化率,有高中数学基础的话,应该很熟悉。)
大部分人最早接触的导数是这个:

它反应不出对正弦函数(余弦函数)求导的真正意义:

对写成复指数形式的波函数求导数时,只需要乘一个虚数单位i。
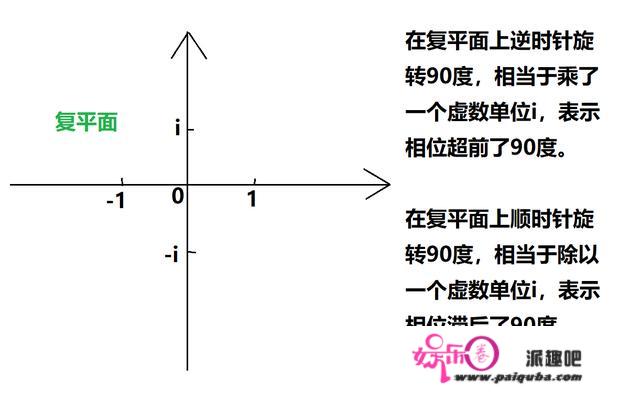
乘一个虚数单位i,就表示相位超前了90度。
除以一个虚数单位i,就表示相位滞后了90度。

这个公式的意义也在于此。
物质波的波函数和经典的波函数一比较,会发现:
德布罗意方程组并没有完整地描述物质波。
(没有把波的要素整合到一起。)
想要完整地描述物质波,就需要写出物质波的波函数。
有了前面的铺垫,这一步非常简单。
直接把德布罗意方程组代入经典的波函数就行了!
可以得到:
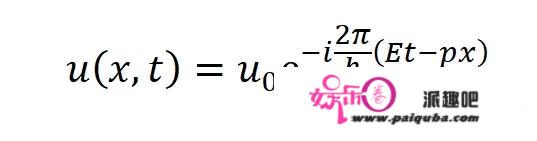
(用能量和动量分别替换经典的波函数中的频率和波长。)
还可以定义一个约化普朗克常数:
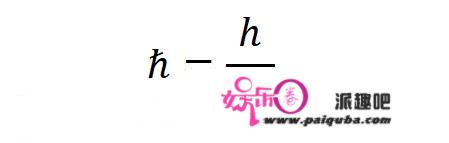
让波函数变成:

由于物质波很特殊,所以用一个专门的符号Ψ来表示物质波的波函数:
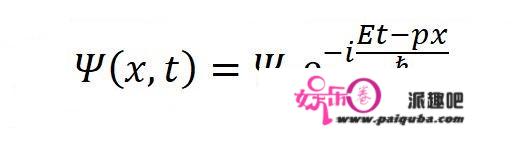
也可以写得简单一点:
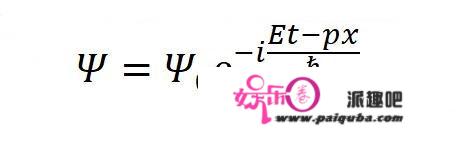
你经常在科普量子力学的作品中看到的那个Ψ,就是这里的波函数。
每个波函数,都描述了一种物质波。
经典的波动方程波函数有了,那波动方程该怎么写?
别急,咱们先看另一个问题:
我知道有人会问:
波函数不是已经可以描述物质波了吗,为什么还要再写个波动方程?
简单地说,波函数是个代数方程,而物理学家需要的波动方程是个微分方程。
说白了,波函数只是表像,而波动方程才是内在的规律。
(说得数学一点,代数方程只是表像,而微分方程才是内在的规律。)
从波动方程出发,可以求解出各种各样的波函数。
就像从牛顿第二定律出发,可以求解出各种各样的运动轨迹。
(这个类比非常恰当,微观粒子的波函数就相当于宏观物体的运动轨迹。)
而薛定谔要构建的,就是可以比肩牛顿第二定律的波动方程。
换言之,薛定谔方程之于量子力学,犹如牛顿第二定律之于经典力学。
那这个波动方程到底该怎么写?
还是要借鉴经典力学。
先观察一下经典的波动方程。
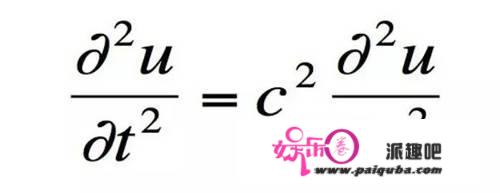
当然,这是一维波动方程。
u是波函数,是关于t和x的函数。
c是波速。
(至于推导过程,够写一篇长文了,笔者在此略过。)
它有什么特点?
首先,有个等号。
其次,等号两边分别让波函数对时间和距离求二阶偏导数。
至于什么是偏导数,可以按物理意义理解成变化率。
(偏导数和导数只是名字不同,并没有实质上的差别。)
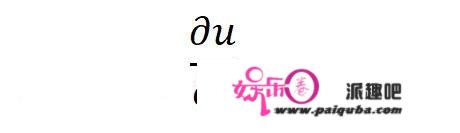
上面这个式子是对时间求偏导数,表示的是波函数随时间变化的快慢。

上面这个式子是对距离求偏导数,表示的是波函数随距离变化的快慢。
求一个偏导数以后,还可以再对偏导数求偏导数,这就是二阶偏导数。
比如,对时间求二阶偏导数:
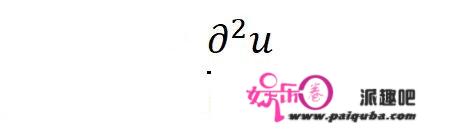
对距离求二阶偏导数:
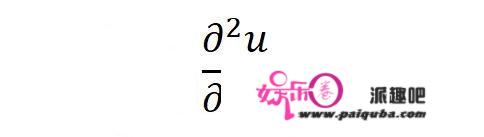
(具体内容够写半本微积分教材了,笔者在此略过。)
那好,咱们先把物质波的波函数对时间和距离求偏导数,再看看能构建什么样的等量关系。
上面说过,物质波的波函数长这样:

求偏导数以后,会惊奇地发现:
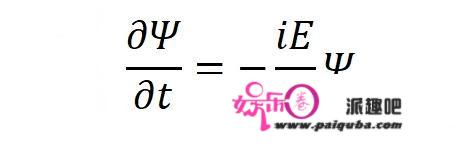
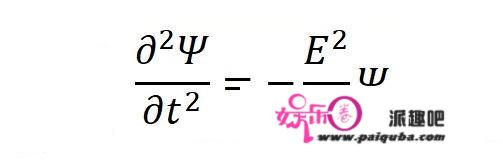
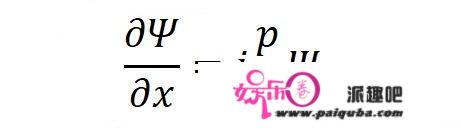

求偏导数之后,物质波的能量和动量被提取出来了!
(至于具体怎么计算偏导数,也够写一篇长文了,笔者在此略过。)
如果可以找到能量和动量的等量关系,那不就搞出了波动方程吗?
(没错,就是依葫芦画瓢!)
经典的能量-动量关系能量和动量有什么等量关系?
在经典力学里,有两种运动的量度:
动能:决定物体可以运动多长距离。
动量:决定物体可以运动多长时间。
动能是它:

动量是它:

m是物体的质量。
v是物体的运动速度。(暂且不考虑向量)
很容易看出,它们之间有着这样的关系:

但我们需要找的是能量和动量的关系,而能量不只包括动能。
所以需要把上面式子的等号两边都加上势能。
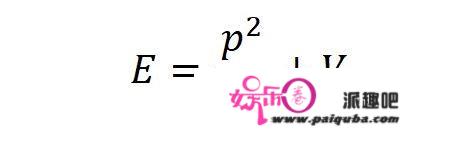
V是势能。
(对于微观粒子,按照经典力学的框架,没有内能一说,所以微观粒子的所有能量就是动能和势能。)
这样就得到了经典的能量-动量关系。
写出薛定谔方程把求偏导数得到的物质波的能量和动量代入经典的能量-动量关系,就得到了薛定谔方程!
具体的做法是:
观察上面求偏导数的结果,会发现:
求偏导数之后,得到的是能量或动量与波函数的乘积。
求二阶偏导数之后,得到的是能量或动量的平方与波函数的乘积。
所以我们先把经典的能量-动量关系两边乘一个波函数。

再从上面求偏导数的结果中整理出:
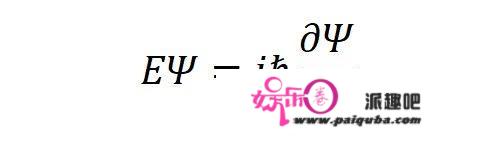
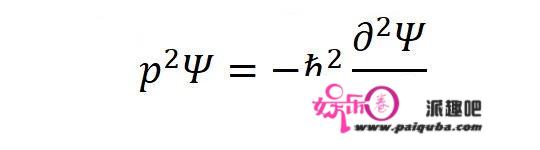
将这里的三个公式合在一起,就写出了薛定谔方程!
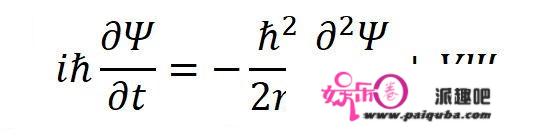
(推导方法不唯一,文章里的推导方法仅供参考。)
和经典的波动方程对比一下:
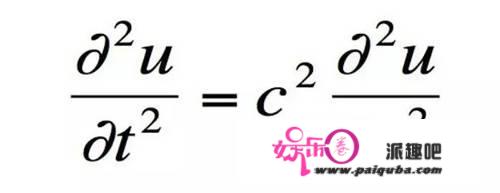
会发现薛定谔方程只对时间求了一阶导数,而波动方程必须要求对时间求了二阶导数。
怎么办?
不用慌,还记不记得乘一个虚数单位i代表什么?
求导!
这就是使用复指数函数的巧妙之处!
这样一来,薛定谔方程的左边也是求了二阶导数,薛定谔方程是波动方程!
当然,刚刚推导的只是一维的薛定谔方程。
里面的波函数也是一维的波函数:
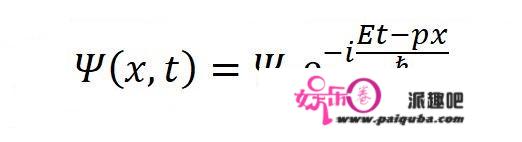
而空间有三个维度:
动量也有三个分量:

依葫芦画瓢,三维的波函数是:
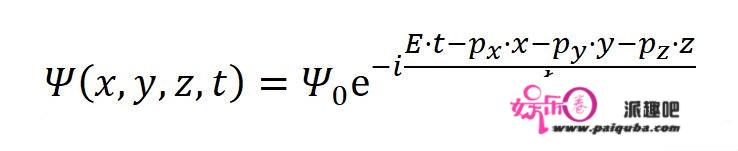
在经典的能量-动量关系中,出现了动量的平方。
而动量的平方与其各个分量之间有着这样的关系:
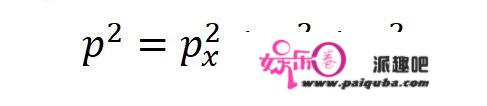
所以,三维的薛定谔方程是:
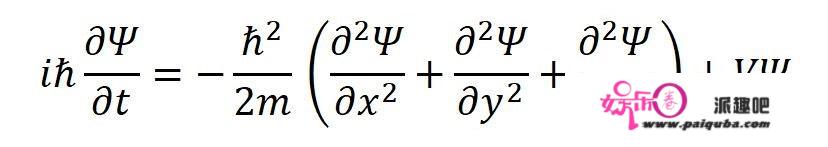
(能看懂一维的薛定谔方程的推导过程的话,在这里推导三维的薛定谔方程也就不成问题了。)
三维的薛定谔方程还可以写成这样:
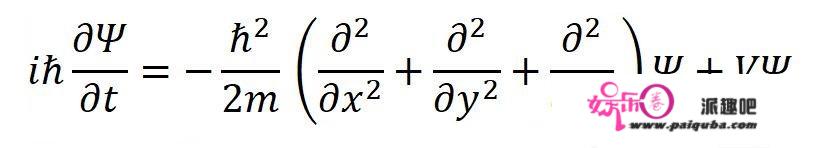
写成这样是为了定义拉普拉斯算子:
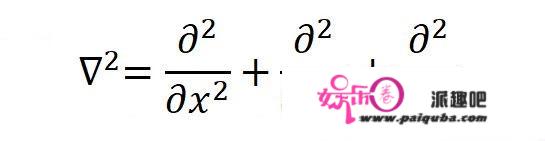
这样一来,可以用拉普拉斯算子把三维的薛定谔方程写成:

也可以写成:
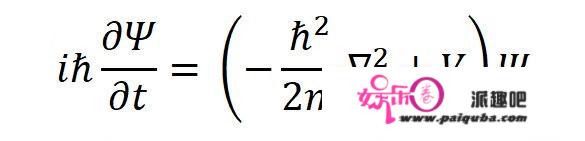
写成这样是为了定义哈密顿算符:
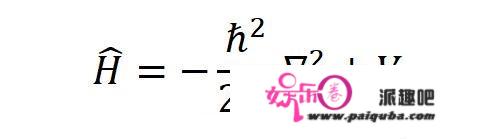
用哈密顿算符来写薛定谔方程:
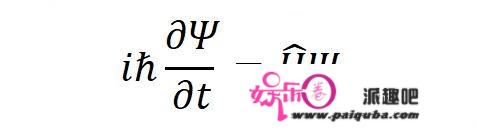
这基本上就是薛定谔方程的最简形式了。
当然,如果物质波的能量不随时间变化,还可以写成定态薛定谔方程:

(定态,就是能量不随时间变化的意思。)
薛定谔方程等号两边的量,本来就是能量乘波函数。
概率波诠释上面提到过波的五个要素,我们考虑了其中的四个要素:
幅值、相位、频率、波长。
对于物质波,频率表示能量、波长表示动量、相位用于比较波与波之间的先后顺序。
那幅值呢?
玻恩参透了这个秘密:
波函数的模平方,是微观粒子出现的概率密度。

(有向量的基础知识,就知道什么是模、什么是模平方。)
所以说,物质波是一种概率波。
既然是概率,就有个归一化条件。
名字有些吓人,其实就是说:
微观粒子出现在所有位置的概率之和为1。
另外,上面的波函数是基于简谐波写出来的,而任意波形的波都可以由一系列的简谐波叠加而成。
所以说,波函数是可以叠加的。
薛定谔方程的意义薛定谔方程的建立,意味着波动力学诞生了。
而量子力学就是由矩阵力学和波动力学合并而成的。
(矩阵力学着眼于粒子,而不是波,和波动力学在数学上是等价的。)
那个时候,才算是有了量子力学。
就像相对论和相对论动力学还差得远一样,量子论和量子力学也还差得远。
(笔者在上一篇问答作品中提到过:相对论和相对论动力学还差得远。)
很多介绍量子力学的教科书和科普作品都把普朗克的量子化假设作为开端,并称普朗克为量子之父。
这种做法确实合情合理,但也让不少人产生了误解:
普朗克提出量子化假设以后,量子力学就诞生了。
普朗克是量子力学之父。
而事实是:
普朗克提出量子化假设以后,量子论诞生了。
普朗克是量子论之父。
量子论是微观世界的一个总体框架,而量子力学是依据这个框架建立的动力学理论。
写出基于量子论的动力学方程,才算是有了量子力学。
薛定谔方程就是其中的一个动力学方程。
另外,薛定谔方程可以描述电子,而化学反应不过是原子最外层电子(价电子)的把戏。
所以,原则上,可以用薛定谔方程计算一切化学反应的结果。
量子化学也因此而生。
薛定谔方程的缺陷其一,上面有个标题是经典的能量-动量关系,薛定谔方程是基于它建立的。
也就是说:当微观粒子高速运动时,薛定谔方程就不可靠了。
解决方法:按相对论的能量-动量关系建立波动方程,就可以描述高速运动的微观粒子了。
其二,薛定谔方程没有考虑微观粒子的自旋。
而电子、质子、中子、……,这些微观粒子都是有自旋的。
解决方法:引入泡利矩阵。
这两个缺陷最终被狄拉克方程一举解决。
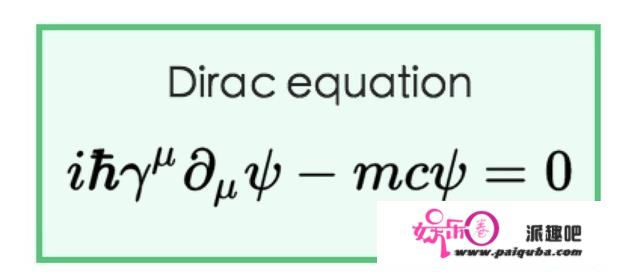



我来回答