为什么黑洞会发光?霍金辐射背后的物理学,最硬核的解释

根据爱因斯坦的经典引力理论,黑洞是一个时空区域,它具有极强的引力场,任何东西都无法逃脱(即使是光也不能)。这个性质的一个结果就是黑洞永远不会缩小。然而,如果考虑量子效应,这种情况就会发生巨大变化。正如这篇文章将展示的,由于黑洞表面附近(所谓的视界)的量子场的真空涨落,黑洞会发射出粒子,如光子、中微子和其他粒子。因此,黑洞并不是完全“黑的”。这一突破性的发现者是英国著名物理学家斯蒂芬·霍金。

图1:第一张黑洞图片。这个特殊的黑洞位于M87星系的中心。我们在图像中看到的是围绕黑洞旋转的热气体发出的辐射。静态黑洞发射出粒子的这一预测让物理界感到惊讶。霍金先前的研究表明,旋转的黑洞会产生粒子。后来他发现即使是静止的黑洞也会产生粒子。

图2:斯蒂芬·霍金和他开创性的论文在这篇文章中,我将遵循Mukhanov和Winitzki关于二维时空中无质量标量场的霍金温度的推导(四维时空中的推导可以在霍金的原始论文中找到)。
霍金辐射的物理起源关于霍金辐射起源的标准解释如下。量子涨落的一般特征是虚粒子-反粒子对的不断产生。在黑洞的视界附近经常发生的是,两个粒子中的一个穿过视界,而另一个粒子以霍金辐射的形式逃逸。
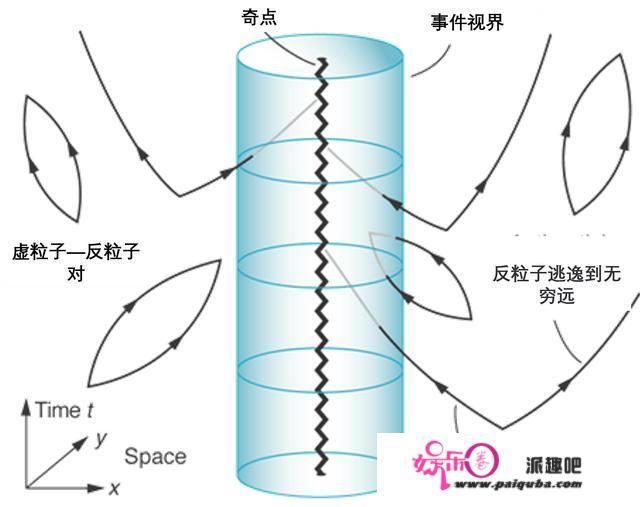
图3:正如文中所解释的,当一对粒子在黑洞附近产生,其中一个落在黑洞里面,另一个粒子以霍金辐射的形式逃逸。虽然这种解释是普遍存在的,但它不符合实际计算。
史瓦西黑洞史瓦西黑洞是非旋转的,是球对称的。它是最简单的黑洞,只包含一个参数,质量m。球面坐标系下的二维史瓦西线元为:

式1:二维的史瓦西线元。式1似乎表明在史瓦西度规中有两个奇点(时空中引力场变得无穷大的位置),一个在r=0处;另一个在r= 2M处,也就是所谓的史瓦西半径。更具体地说,代入r= 2M,线素的两个分量为:

式2:史瓦西度规张量在r=2M处计算的(t,r)坐标中的分量然而,接下来我们将会看到,史瓦西黑洞的唯一物理奇点是在r=0处。在r = 2M处的奇点实际上只是一个坐标奇点,可以通过一个新的坐标系来消除。为了证明这一点,我们将引入Kruskal-Szekeres坐标。

图4:由史瓦西黑洞产生的引力透镜效应(发生在遥远光源和观察者之间的物质造成的光线弯曲),该黑洞穿过视线平面到达一个星系Kruskal-Szekeres坐标得到的Kruskal-Szekeres坐标如下。首先,定义“tortoise坐标”r*(r)和相应的tortoise光锥坐标:

式3:tortoise坐标和tortoise光锥坐标的定义。注意r*在r = 2M处是奇异的。这意味着tortoise光锥坐标,在r = 2M处也是奇异的,不包括r < 2M的区域,这被定义为黑洞内部。为了覆盖整个史瓦西黑洞时空,我们需要再次改变坐标系。这个新的坐标系将是Kruskal-Szekeres光锥坐标的解析扩展,其定义如下:
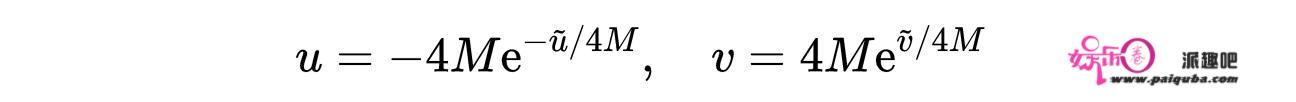
式4:Kruskal-Szekeres光锥坐标。线元素变成:
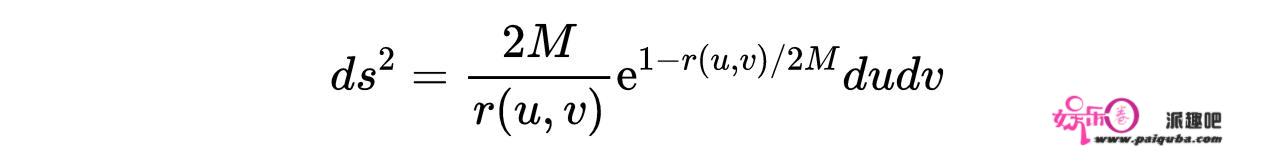
式5:式4中Kruskal-Szekeres光锥坐标中的线元素。我们注意到r=2M处没有奇点。现在将它与式1进行比较。我们看到在这个坐标系中,史瓦西半径r=2M处的奇点消失了。因此,如前所述,r = 2M是一个坐标奇点,而不是一个物理奇点。这意味着当一个自由落体的观察者穿过半径r = 2M时,他不会感到任何异常。
注意Kruskal-Szekeres光锥坐标的有效域为-∞< u <0 和 0 < v < ∞。这些坐标不覆盖 r < 2M区域。换句话说,对于 r >2M,它们只在黑洞之外有效。但是,请注意,线元方程5在所有-∞< u <∞ 和 -∞ < v < ∞区域的定义是明确的,覆盖了所有的史瓦西时空。然后我们必须解析地扩展坐标u和v,使其包含u > 0 和 v < 0。
根据Mukhanov和Winitzki,我们可以用式3、4和5将新的Kruskal-Szekeres光锥坐标(u, v)表示为原来的(t, r)。我们得到以下两个关系:
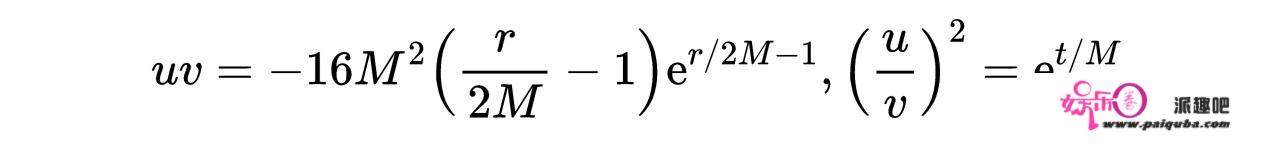
式6:用t和r表示的Kruskal-Szekeres光锥坐标。如果我们继续解析u和v,这些关系将适用于所有的史瓦西黑洞时空。
为了得到史瓦西黑洞的Kruskal-Szekeres图,我们引入了两个新的坐标,即:
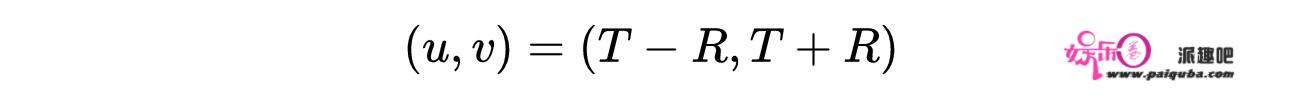
式7:坐标u和v的定义。现在,为了覆盖整个图,我们必须扩展坐标(u, v)。用原始坐标(t, r)表示扩展变量(u, v),我们得到两组坐标,即:

式8:史瓦西黑洞几何上的两组Kruskal-Szekeres坐标。上对坐标覆盖黑洞外部(r >2m),下对坐标覆盖黑洞内部(r <2M)。Kruskal-Szekeres图如下图所示:

图5:Kruskal-Szekeres图,其中轴为坐标(T, R)。史瓦西黑洞时空被划分为四个渐近区域I, II, III, IV。R为常数的曲线为双曲线,T为常数的线为直线请注意以下几个重要特征:
我们知道(u,v)零测地线是斜率为π/4和-π/4的直线由式6可知,超曲面r = const对应于T-R平面上的下列双曲:

式9由式6,对于r > 2M,我们有uv < 0,这意味着方程9中的双曲线r =常数是类时间的。对于r < 2M则相反,uv > 0,式9中的双曲线r =常数是类空间的。
从等式6的第二个表达式中,我们可以看出,曲面t =常数是用直线表示的。 对于r < 2M(在黑洞内部),时间t变成了空间坐标。在外面,t仍然被解释为时间。降维说,在事件视界内,空间和时间有效地互换了!
在T的两个值处有两个奇点:

式10:r=0对应的两个类空间奇点。两个r = 0曲面以外的区域不能被这些坐标覆盖。
量化为简单起见,让我们写出二维弯曲时空中无质量标量场的作用:

式11:具有度规张量g的二维弯曲时空中无质量标量场的作用。对应于S的标量场方程可以用tortoise光锥坐标或Kruskal-Szekeres光锥坐标表示。在这两种情况下,它都是两项的和:

式12:上述作用S对应的标量场方程,用tortoise光锥坐标和Kruskal-Szekeres光锥坐标表示。这是S的正形不变性的结果。a和b是行为良好的函数。下面是一个简单的例子:

用tortoise光锥坐标表示的史瓦西线元素为:
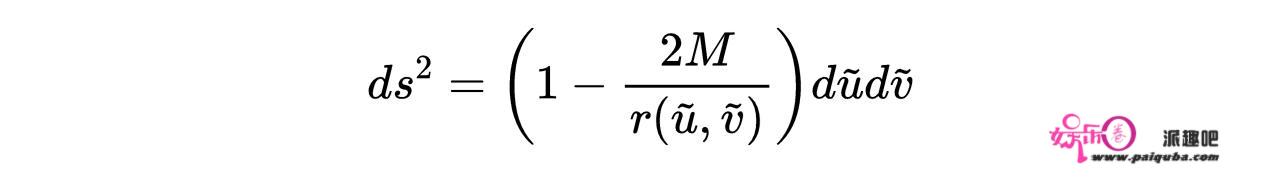
式14:史瓦西线元,用tortoise光锥坐标表示。在离黑洞很远的地方,线元素变成:

式15我们看到,在离黑洞很远的地方,静止观察者的固有时间与式15中的t重合。
在量子场论中,我们通常用创造和湮灭算符来扩展场:
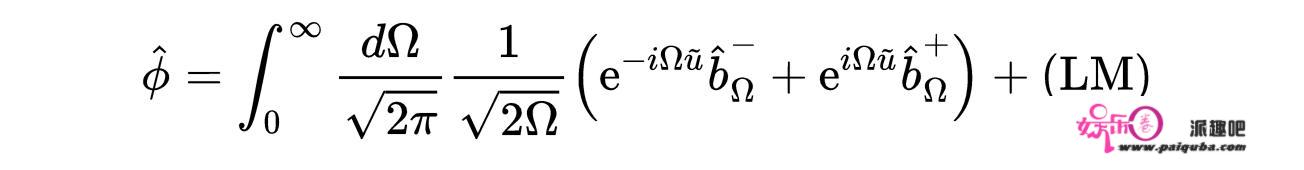
式16:场ϕ的扩展。对应于b湮灭算符的真空称为Boulware真空,根据距离黑洞很远的观察者的说法,它不包含任何粒子:

式17:Boulware真空。因为,正如我们之前看到的,tortoise光锥坐标只覆盖了史瓦西黑洞时空的一部分(视界外),Boulware真空在视界上有奇异的行为,因此它在物理上是无效的。此外,相应的能量密度会在视界处发散,量子涨落会产生强烈的反向反应,从而推翻弱扰动经典引力场的基本假设。
与tortoise光锥坐标相比,Kruskal-Szekeres光锥坐标覆盖了所有的史瓦西黑洞时空,并且在视界上定义明确。在视界附近,Kruskal-Szekeres坐标中的线元素为:

式18:视界附近的Kruskal-Szekeres光锥坐标中的线素。因此,一个穿过视界的观察者与一个频率为ω > 0的模式有关。再次如式16所示扩展场,我们得到:

式19:使用Kruskal-Szekeres光锥坐标定义相应的产生和湮灭算符的场ϕ的扩展。非奇异真空状态现在有一个有限的能量密度,导致量子涨落的一个小反向反应,保持经典引力场正常扰动。Kruskal 真空服从:
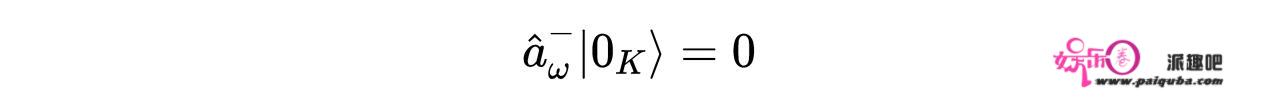
式20:Kruskal–Szekeres真空所服从的条件。因此,可以被认定为接近黑洞的“真正”真空。
现在,对于遥远的观察者来说,Kruskal–Szekeres真空中含有粒子。我们得到远处观测者测得的热谱和相应的霍金温度的表达式如:
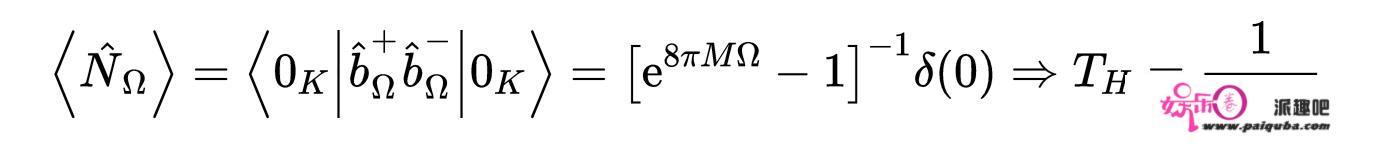
式21:远端观测者测得的热光谱和相应的温度(即所谓的霍金温度)。霍金辐射非常微弱,被大量的热气体发出的辐射所淹没,这些气体落入我们目前确认的所有黑洞中。

图6:一颗恒星被一个被尘埃环包围的黑洞吞噬的发光物质流。这可能是它尚未被观测到的原因之一。由式21可知,只有质量很小的黑洞才会发出可测量强度的霍金辐射。
想了解更多精彩内容,快来关注老胡说科学



我来回答