为什么光子没有量量，还能够被黑洞吸引？

学过物理的可能晓得，光子没有静行量量，依据牛顿的万有引力定律，光是不成能被黑洞吸引的。那为什么黑洞能够吸引四周的光呢？

先来熟悉光

光是我们熟悉世界的信使。光是物理学中讨论最多的对象之一，从牛顿的微粒说与惠更斯的颠簸说起头，关于光的水平的争论继续了上百年。之后，麦克斯韦同一了光和电，证实了光也是电磁波，电磁波也是以光速传布的。实空中的光速不只是宇宙中最快的速度，仍是物体运动速度的极限。

20世纪初爱因斯坦提出了光量子的概念，以此为根底阐明了光电效应，因而获得了诺贝尔物理学奖。后来科学家发现，光具有波粒二象性，光既能够看做粒子，又能够看做波。德布罗意发现不只光具有波粒二象性，电子等微不雅粒子也具有波粒二象性，好比光会发作衍射，电子也同样会发作衍射。从波的角度来看，光就是电磁场的颠簸。

上图为电子衍射照片

进进量子力学的世界后，科学家们发现光子还有一个重要的感化，就是充任电磁力（或电磁彼此感化）的前言粒子，粒子之间通过交换虚光子传递电磁彼此感化。

光有没有量量？

经严酷的科学尝试证实，光是没有量量的，严酷来说没有静行量量。天然界中除了光子，传递强力的胶子也是没有静行量量的。

不外光却拥有能量，光所照顾的能量的大小与它的频次有关，频次越高，光的能量越大。即E=hv，此中h为普朗克常数，v暗示光的频次。此外光的频次越高，光的粒子性就越显著。

爱因斯坦从狭义相对论中推导出的量能方程告诉我们：量量和能量是物体统一性量的两种区别度量体例，能量和量量是高度同一的，有能量的物体便具有量量，有量量的物体也拥有能量。按照量能方程E=mc^2，即可推导出光的量量为hv/c^2，光的那种量量被称之为动量量或者相对论量量。

依据相对论的描述，物体的运动速度越快，其所具有的动能也就越大，响应地量量也会越大。不外，只要当物体的运动速度接近于光速时，其量量才会发作明显的改动，在低速形态下那种改动能够漠视。恰是因为光子的静行量量为0，光从降生之时就以光速运动，不需要加速。而当物体有静行量量时，运动速度到达光速，量量就会变得无限大，显然物体的运动速度一定不克不及到达以至超越光速。

上图为相对论量增效应公式

因为光没有静行量量，只要能量，我们经常将光​当做​纯能量物量对待，光就是能量的载体。例如：正电子和负电子发作湮灭反响会百分百转化为能量，那里的能量其实就是光，正反电子湮灭后会转化为光子。太阳会发光发热，太阳的光和热就是通过电磁辐射的形式传到地球上的，也就是光。凡是我们所说的光是指可见光，其它频段的电磁波也能够称之为光。

所以，我们能够认为光是有动量量的。

光为何会被黑洞吸引？

上面已经说过了，光具有动量量，那么是不是就能够操纵万有引力来阐明呢？

动量量那一概念确实能够阐明光为什么可以被黑洞吸引，但却存在局限性。一般而言，光在实空中是沿曲线传布的，当光线被黑洞吸引时便会发作偏折。典范力学也能推测到那一现象，但对偏折角的估量却其实不正确。要想切确，就需要采纳更完美的理论，相对论力学即是目前认为最完美的理论。

按照相对论的推测，当光线颠末太阳四周时，在太阳的引力感化下，光会产生轻细的偏折，计算出的光线偏折角为1.75角秒，而按照牛顿引力理论计算出来的偏折角则为0.87角秒。在20世纪初，由爱丁顿等人指挥的科学团队对此现象停止了屡次丈量，切确的尝试成果表白：爱因斯坦是对的！

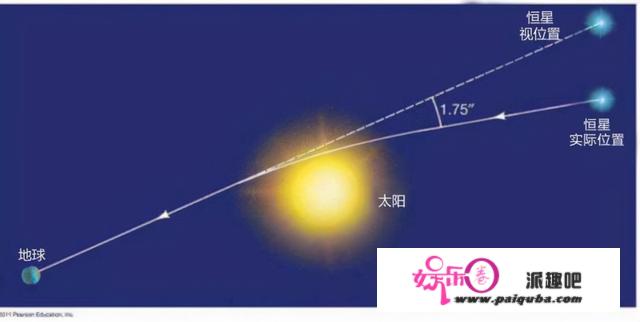
在相对论中，爱因斯坦丢弃了牛顿的引力概念，或者说不需要引力那个概念了。爱因斯坦引进了空间弯曲的概念，认为引力的水平现实上是空间弯曲。量量越大的物体，对空间的弯曲水平也就越大。

如图所示，空间弯曲招致的光线偏折现象

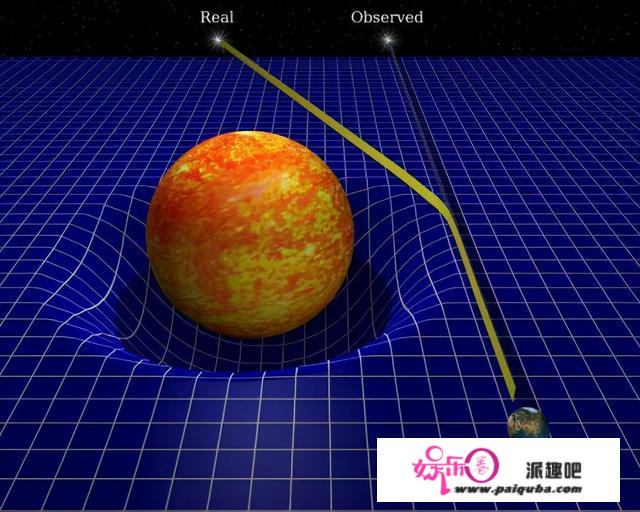
凡是我们认为光是沿曲线传布的，现实上光是沿空间中的测地线（两点之间最短间隔）传布的。当空间被弯曲，光也就只能跟着走曲线，于是在我们看来光就被黑洞吸引了。现实上它们之间其实不存在力的感化，在此根底上，光有没有动量量也就无所谓了。光线被恒星偏折时，偏折角只与恒星的量量有关，与光的动量量无关。

黑洞是一个秘密的天体，因为黑洞外表（视界面）的逃逸速度大于光速，当光闯进黑洞里面就再也出不来了，因而用传统天文不雅测 *** 是看不见黑洞的，需要用到引力波。理论推断，黑洞中心有一个密度无限大、体积无限小的奇点。在人类还没有发现黑洞之前，科学家就从相对论中推导出了黑洞的存在，黑洞内部的空间被无限弯曲，时空曲率无限大。

现实上，任何有量量的物体都可以使空间弯曲，不外只要像太阳、黑洞如许的大量量天体才气够使空间产生较大的弯曲效果，人类才气够发现光线偏折现象。在我们看来，光被那些强引力源吸引了。

如图所示，光掉进了黑洞

结语 由此可见，不管光有没有量量，城市被黑洞吸引，因为黑洞四面的时空弯曲​的​很凶猛，以致于连光也要走曲线。

通过那个问题，让各人熟悉到了相对论力学为什么比典范力学愈加完美。传统的典范力学具有局限性，只适用于低速、弱引力场下的宏不雅运动，要想正确描述高速、强引力场下的情状，就需要相对论出马了。