虫洞能穿越时空，是实在可能仍是科幻假设？

许多人都应该传闻过“虫洞”，无论是从科幻角度可穿越时空的遐想，亦或是从理论物理学前沿的学术新闻里感应不明觉厉，可虫洞事实是什么？它若何成为毗连时空的构造，只是物理学家的玩具吗？事实上，近年来在量子引力的研究中，虫洞躲藏着我们仍未发现的深意。

撰文 | 安宇森

虫洞（wormhole）是一种奇异的时空构造，同时物理学的研究也愈加证明，虫洞是毗连量子理论和引力理论的钥匙。本文拟从洛伦兹（包罗时间和空间）虫洞和欧几里得虫洞两个方面，来介绍虫洞那一根本概念，及其在理论物理学中的感化

虫洞和欧几里得虫洞两个方面，来介绍虫洞那一根本概念，及其在理论物理学中的感化。

洛伦兹虫洞

起首，我们介绍洛伦兹虫洞。洛伦兹虫洞是时空中可能存在的虫洞构造，它是实在存在的物理客体。

关于⾍洞最早的研究启发⾃卡尔·萨根的⼩说《接触》（），那本⼩说也被胜利的影视化了，由罗伯特·泽⽶吉斯指点的同名影⽚《超时空接触》（Contact）⼴受好评。在最后⼩说的原稿中，做者利⽤⿊洞来实现时空隧道。但是其老友Kip Thorne却表⽰担忧，做为研究⼴义相对论的⼤家，他很清晰⿊洞是很难做为时空隧道那种构造的。但是那激发了Kip Thorne的研究兴趣，从⽽后来开展了最后关于⾍洞的⼀系列研究。

虫洞和能量前提

时空穿越是科幻喜好者⼀个永久的兴趣，⽽可穿越的⾍洞似乎是实现它的⼀个很好的途径。因而⾍洞研究的⼀个重要的⽅⾯，即研究它的可穿越性。凡是的⼴义相对论研究中，都是晓得⼀个物量散布，然后研究那个物量散布会给出的时空外形；然⽽虫洞研究中，物理学家的⽬的是实现特定的时空外形——因而Morris和Thorne考虑反其道⽽⾏之，先给出关于时空构造的限造，然后再通过爱因斯坦场⽅程进⾏物量散布的求解。

最后的计算是在球对称坐标系下进⾏的，他们发现若是要想满⾜特定的⾍洞时空构造，那么所需要的物量散布⼀定是违背能量前提的，通俗地来讲，需要引⼊奇异的负能物量。那件工作能够通过测地线汇的法子很⾃然地看出来。⼀般在⼴义相对论中，为了探究时空的⼀些性量，通过测地线汇的变革能够在不解爱因斯坦⽅程的情况下，就可以得出⼀些结论。例如那⾥，若是需要⼀个⾍洞构造毗连两个差别的时空区域并可实现穿越，那么通过它的光线需要先会聚到⾍洞的喉部（即虫洞构造中的最窄处），再从喉部发出。广义相对论中，光线的会聚仍是发散，能够通过类光测地线汇的膨胀给出，描述它的方程凡是叫做Ray-Chaudhuri⽅程，方程如下：

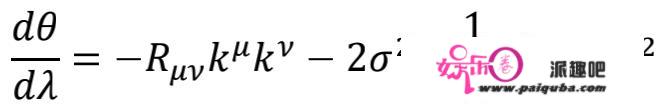
我们能够选择，满⾜扭转和剪切都为0的线汇，σ=ω=0，如许按照通过⾍洞的线汇的特征，可知在⾍洞的喉部⼀定存在 dθ/dλ=0 的位置，那暗⽰了如下的⽅程：

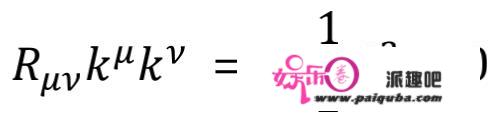
再按照⼴义相对论可知：

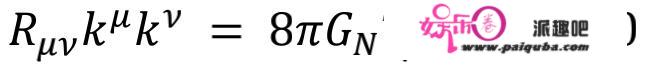
那便毁坏了类光能量前提，因而⾍洞的存在⼀定需要在它的喉部引⼊负能量的奇异物量。

那种奇异物量的引⼊让⾍洞的构造变得⾮常困难，那种违背类光能量前提的物量⼀般只要量⼦理论中才会允许，且凡是⼗分微⼩。同时若是满足⾍洞能够通过，我们还需要考虑⾍洞感化于⼈体所产生的潮汐⼒效应，在⼈体能够忍耐的潮汐⼒的前提之下，理论预⾔⾍洞将会⾮常巨⼤，⽽那么巨⼤的空间都存在奇异物量将其⽀撑，显得更为困难。不外，或许正如科幻⼩说《三体》梦想的那样，⽆限兴旺的⽂明能够在物理定律允许的前提下，不受手艺壁垒的限造做到任何工作——建造⾍洞那种工作仍然能够憧憬。

虫洞与时间机器

既然⾍洞能够看做宇宙中毗连遥远两点之间的近路，那么或许⾍洞能够被革新为时间机器。在时间机器的讨论中，我们忽略⼀些细节，只把⾍洞看成是毗连时空中（t, 0)和（t, L）两点之间的机器，⾍洞的入口对应(t,0)，⽽出口对应(t,L)。若是我们让出口相关于入口进⾏⾼速运动，那么按照狭义相对论的钟慢效应（如双⽣⼦佯谬），出口和⼊口之间就会构成⼀个时间差T；然后我们缩短空间间隔L为0，让出口和⼊口回归⼀点，那么从⼊口到出口，时间就会发⽣⼀个T的跃变，⽽那就完成了穿越到过去或者将来的操做。那即是通过⾍洞构建时间机器的⼀个最简化的版本。

时间机器或许相⽐于⾍洞，更能激发⼈们的兴趣，因为⼈⽣老是充满着各类各样的遗憾。当⼈⽣⾏⾄老年末年，也有各类各样的懊悔，时间机器或许就能够给⼈⼀次从头来过的时机，来填补那些遗憾。因而⽆数凄美动⼈的恋爱故事，都能够在此布景下铺展开来。

然⽽时间机器的呈现会引发良多因果性上的难题，因而在⼤大都时候，时间机器只被看做是玩闹，⽽⾮正经的科学研究课题。或许“⾃然憎恨时间机器”，⽽物理学家们需要做的就是找到响应的物理原理，来证明时间机器不成能被造成。

虫洞与量子纠缠

1997年，Maldacena带着他的AdS/CFT原始论⽂，给理论物理学界炸响了⼀颗惊雷，从此越来越多的学者起头研究引⼒的全息性量。后来，基于Maldacena 2001年的论⽂结论，Raamsdonk⾸先通过简单的论证发现，⾍洞和量⼦纠缠具有素质联络，即ER=EPR料想。(ER=EPR那个名号，是2013 年经Susskind和Maldacena的⼯做正式提出，⽬的是处理⿊洞的⽕墙问题。) ER指代爱因斯坦-罗森桥，它是毗连两个⿊洞之间的区域，能够看做是⾍洞研究的前⾝。不外它是不成穿越的，任何穿越爱因斯坦-罗森桥的行为，都不成制止的落⼊⿊洞奇点。EPR指代的则是量⼦纠缠。

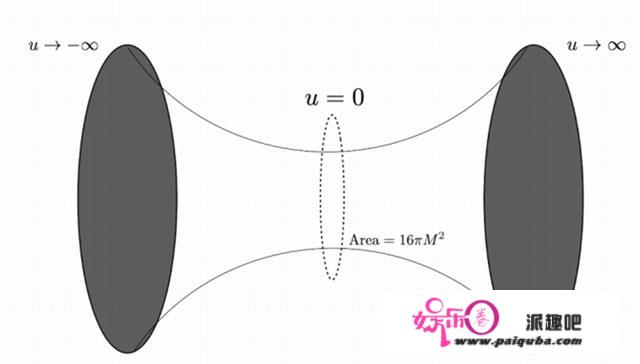
爱因斯坦-罗森桥丨图⽚来源：arXiv: 2110.14958

下⾯我们简单介绍那⼀概念，2001年，Maldacena的研究⼯做发现，量⼦场论中的热场⼆重态TFD：

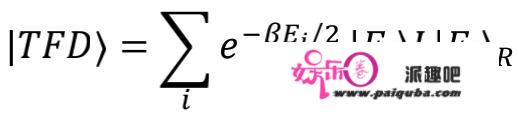
对应于⼀个响应的AdS史⽡西⾍洞，它的彭罗斯图和史⽡西⿊洞的最⼤解析沿拓的彭罗斯图一致。当然，若是盯着彭罗斯图的某个空间截⾯来看，它能够理解为两个通过中间的⾍洞构造毗连的⿊洞。

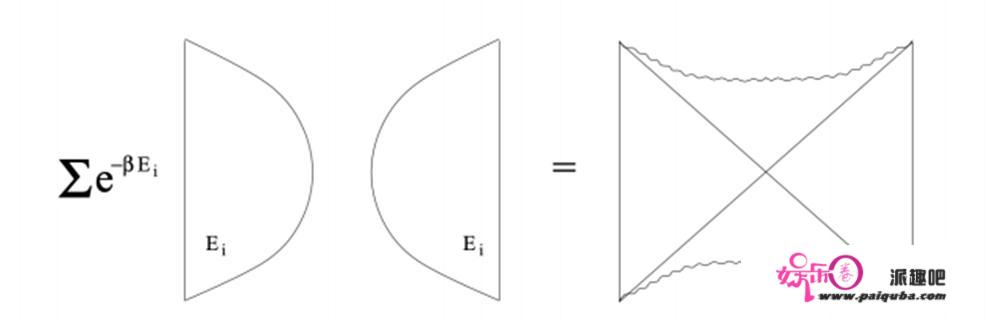
热场⼆重态和史⽡西⿊洞的对应丨图⽚来源：arXiv: 1005.3035

⼈们发现，那个热场⼆重态是⼀个纠缠态，⽽调理温度（也就是那⾥的β)，就对应于调理了摆布两边的纠缠。当温度很低时，上⾯的纠缠态会酿成没有纠缠的曲积态；当温度很⾼时，它会成为最⼤纠缠态。研究发现，跟着温度从高到低的变革，虫洞构造中间的喉会逐步变窄曲⾄断开。因而我们发现从鸿沟理论的视⾓来看减⼩纠缠的那个操做，对应于减⼩两个⿊洞之间毗连⾍洞的⼤⼩。因而那暗⽰了量⼦纠缠和⾍洞具有深入的联络，甚⾄于说它们素质上便是⼀回事。

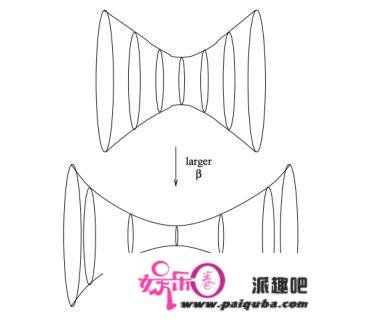
⾍洞的外形跟着温度的降低逐步变窄丨图⽚来源：arXiv: 1005.3035

ER=EPR料想暗⽰了时空本源可能来⾃量⼦纠缠。凡是描述量⼦纠缠的度量是纠缠熵，但是ER bridge的增长时间却会⼤⼤的超越热平衡时间（⽽热平衡之后纠缠熵会趋于定值），因而熵的概念似乎很难描述ER bridge的体积的变革。据此物理学家提出⼀种可能具有和熵差别性量的物理量与⾍洞体积产⽣联系关系，即计算复杂度。它的物理含义是指定⼀系列操做门，从⼀个初态造备到末态所需要⽤到的最⼩操做门的数⽬。

同时，有趣的是，固然前⽂提到的爱因斯坦-罗森桥不成穿越，但是我们能够构造响应的模子来实现那⼀可穿越⾍洞，即在鸿沟引⼊⼀个叫做double trace deformation的操做，引⼊如下的算符扰动。那个操做相当于给布景时空引⼊了⼀条负能量的能流，它的能量在⿊洞视界附近因为引⼒蓝移会变得⾮常⼤，因而会关于布景形成很⼤的反做⽤，从⽽影响视界的位置，使得⿊洞的视界向内收缩。因而从⼀个鸿沟发出的，本来落⼊奇点的光⼦会跑到视界外边，从头抵达另⼀个鸿沟。即实现了⾍洞的可穿越性。

按照ER=EPR的思惟，那个过程相当于引⼒版本的量⼦隐形传态，⽽double trace deformation则类似典范信道。在量⼦隐形传态中，似乎量⼦⽐特是通过量⼦纠缠在另⼀个地⽅被从头构造出来的；⽽在引⼒的图像下，它有了⼀个全新的理解，那就是它是通过毗连两个地⽅的⾍洞穿越⽽来的。

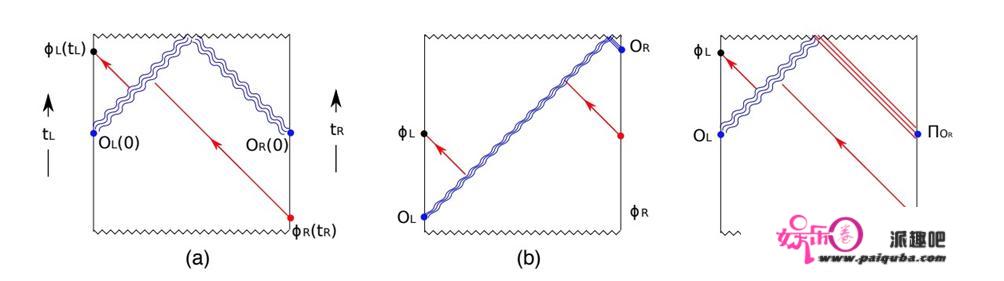
可穿越⾍洞的物理图像丨图⽚来源：arXiv: 1704.05333

欧几里得虫洞

以上介绍了时空中的⾍洞做为⼀个可能物理客体所需要具备的前提及其响应的物理。然⽽，在近⼏年的量⼦引⼒研究中，⼀种新的⾍洞构造激发了⼈们更多的兴趣，即欧几里得虫洞。

介绍什么是欧几里得虫洞之前，我们先介绍理论物理研究中，经常停止的欧式化的操做。通过火析量子场论中的途径积分和统计物理中的配分函数的类似性，我们发现若是对时间停止如下wick动弹的操做t=iτ，（关于wick动弹拜见《温度与奥秘的虚时间 | 寡妙之门》）即将时间坐标虚数化，我们能够将量子场论的问题和统计物理的问题等价起来，由此得到的即欧式途径积分。在欧式途径积分中，并没有时间标的目的，能够看做是某个时间面上的物理。（当然我们也能够将欧式途径积分和洛伦兹途径积分连系起来。）

欧式途径积分是研究浩瀚理论物理问题的一个极为有效的东西。后面我们将介绍，在用欧式途径积分详细的计算黑洞霍金辐射的精细熵的时候，会呈现之前所没有发现的虫洞构造。那种⾍洞构造，能够有助于我们理解浩瀚困难问题，如⿊洞的信息丧失问题。

拷贝虫洞与信息丧失

⿊洞信息问题，是量⼦⼒学和⼴义相对论在⿊洞那个时空下的最深入的⽭盾。考虑纯态物量塌缩为⿊洞继⽽辐射，我们能够看到⼀个从纯态到混合态的⾮⼳正演化，但是它是不被量⼦⼒学所允许的。⿊洞信息问题，做为⼀个会下⾦蛋的母鸡，激发了物理学家们源源不竭的缔造⼒。

比来基于全息纠缠熵的启发，⼈们发现了⼀种在引⼒入彀算霍⾦辐射切确熵的法子，被称做岛屿公式。那种计算得到的切确熵，⼗分奇异的满⾜Page曲线，进⽽满⾜量⼦⼒学的⼳正性。我们晓得，全息纠缠熵的RT公式，起头固然是做为⼀个半料想式的⼯做，但是后来得到了引⼒途径积分的切确证明。⽽那⾥得到的岛屿公式，能否能够通过引⼒途径积分来证明？若是能够的话，那么它应该来⾃于引⼒途径积分中哪些部门的奉献呢？

⾸先我们介绍若何在场论入彀算纠缠熵，它能够通过⼀种叫做拷贝手艺（replica trick）的法子计算，即将研究的系统拷贝n份，进⾏计算，最初再进⾏解析延拓的法子。公式如下：

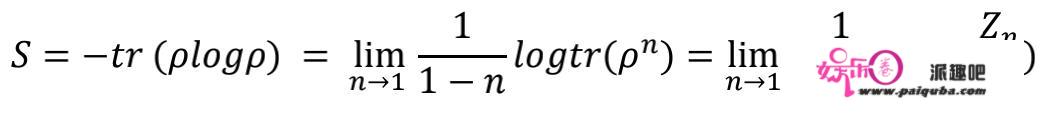
上文第一个等号是纠缠熵的定义，第二个等号则是应用洛必达法例得出的，那一步操做凡是叫做拷贝手艺（replica trick）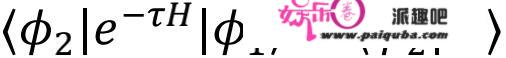

。因为途径积分物理含义描述的是，从初态到末态的概率幅，所以欧式途径积分能够⽤来定义波函数，进⽽定义密度矩阵。在那个欧式途径积分的表述下，上⾯纠缠熵的计算能够转化为在拷贝流形上的配分函数的计算，即上⽂的最初⼀步等式。

根据上面的思绪，若是我们将霍⾦辐射的密度矩阵通过欧式途径积分进⾏⼀个图形表⽰的话，切确地计算它的熵（即配分函数）需要考虑所有可能的拷贝流形构型。考虑辐射和⿊洞整体构成⼀个纯态，因计算的是霍⾦辐射的熵，需要将⿊洞部门求迹。

熵的计算只是要求辐射密度矩阵做为鸿沟⾸尾按序毗连构成⼀个replica的构造，但其几何内部其实⽆法进⾏限造，因而计算Z时需要考虑所有可能的内部构型，包罗⼀些连通的构型。

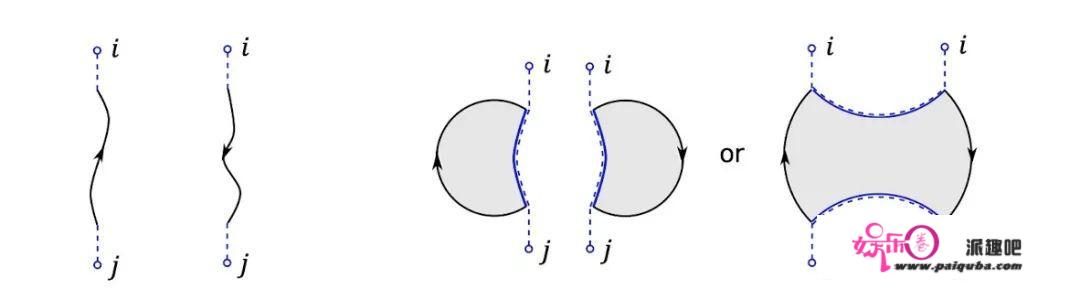
⼀个简单的⽰企图：左侧来⾃辐射密度矩阵构成的鸿沟前提（实线代表做了求迹之后的⿊洞鸿沟，虚线代表辐射），右侧代表计算所需要的引⼒构型。第⼀个图是⾮连通的构型，第⼆个图代表连通的拷贝⾍洞构型。图⽚来：arXiv: 1911.11977

当不考虑连通构型之时，能够得到和霍⾦最后的计算相符的熵，此时违背⼳正性；⽽考虑那个连通的构型（凡是叫做拷贝⾍洞），则会得到和⼳正性预期相符的熵的⾏为。（考虑全连通构型就能够得到岛屿公式在晚期的成果，然⽽实在的拷贝⾍洞的奉献会更丰硕。）那个连通构型它的含义和⾍洞很像，都是通过⼀个连通构造来毗连差别的引⼒区域（只不外那⾥的差别区域是对⼀个别系做replica trick得到的），但是它和洛伦兹型的⾍洞对应的物理却⼤不不异，⽽它详细的物理含义仍然有待更多的理解和廓清。

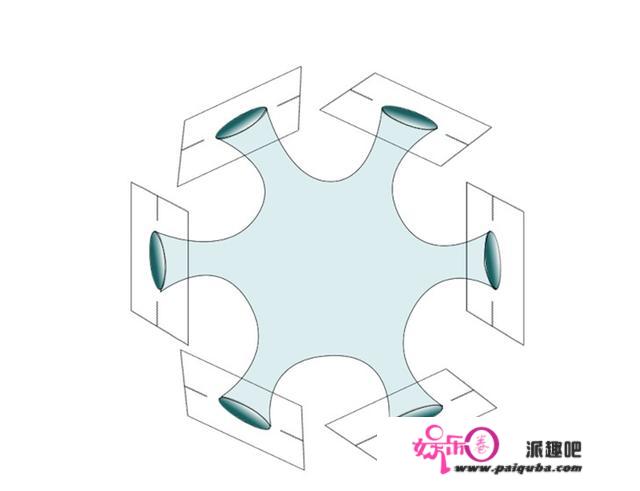
拷贝⾍洞的特点，从图中我们能够看到每⼀个鸿沟⾯上的⿊洞毗连在了⼀起。图⽚来源：arXiv: 1911.12333

拷贝⾍洞的计算是复杂的，此中只要最简单的模子能够考虑Replica⾍洞的所有可能构型，并将其解析的乞降起来得到最为切确的辐射切确熵。然⽽物理学家已经能够（⾄少在2维下）通过拷贝⾍洞的⽅式，证明先前得到的岛屿公式的准确性。拷贝⾍洞的呈现给⿊洞信息问题的研究注⼊了新的⽣机活⼒，良多问题都得以被从头讨论研究，例如引⼒系综对应问题，量⼦引⼒中的整体对称性问题，以及⿊洞辐射事后的剩余（remnant）等。

也许实正有趣的工作才刚刚起头，等待将来⾍洞的研究会带给我们更多的欣喜。

参考文献

[1] M.S. Morris and K.S. Thorne, Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity, Am. J. Phys. 56 (1988) 395.

[2] M.S. Morris, K.S. Thorne and U. Yurtsever, Wormholes, Time Machines, and the Weak Energy Condition, Phys. Rev. Lett. 61 (1988) 1446.

[3] J.M. Maldacena, The Large N limit of superconformal field theories and supergravity, Adv. Theor. Math. Phys. 2 (1998) 231[hep-th/9711200].

[4] J.M. Maldacena, Eternal black holes in anti-de Sitter, JHEP 04(2003) 021 [hep-th/0106112].

[5] M.V.Raamsdonk, Building up spacetime with quantum entanglement, Gen.Rel.Grav(2010) 2323-2329

[6]J. Maldacena and L. Susskind, Cool horizons for entangled black holes, Fortsch. Phys. 61 (2013) 781 [1306.0533].

[7] P. Gao, D.L. Jafferis and A.C. Wall, Traversable Wormholes via a Double Trace Deformation, JHEP 12 (2017) 151 [1608.05687].

[8] A. Almheiri, T. Hartman, J. Maldacena, E. Shaghoulian and Tajdini, Replica Wormholes and the Entropy of Hawking Radiation, JHEP 05 (2020) 013 [1911.12333].

[9] G. Penington, S.H. Shenker, D. Stanford and Z. Yang, Replica wormholes and the black hole interior, 1911.11977.

[10]P.S Hsin, L.V.Illiesiu, Z.Yang，Violation of global symmetries from replica wormholes and the fate of black hole remanants. Class.Quant.Grav.38(2021)19,194004.

转载内容仅代表做者概念

不代表中科院物理所立场

原题目：“奇异虫洞，不行科幻”

来源：返朴

编纂：乐子超人